construction of the platonic solids

OBJECTIVE: To gain an understanding of the geometric make up of form and improve model building skills.

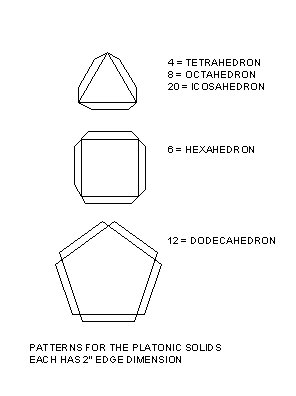
BACKGROUND: The name of the so called "Platonic Solids" comes from the fact that these forms are mentioned by the great 4th century B.C. Greek philosopher Plato (in his Philebus, 51c ff.), as being forms which are "always beautiful in their very nature, and they carry pleasures peculiar to themselves." They are produced by simply combining a given number of regular geometric shapes to produce a 3 dimensional form. There are only five Platonic Solids, which are made up of the following elements:

Tetrahedron: 4 equilateral triangles
Hexahedron: 6 squares
Octahedron: 8 equilateral triangles
Dodecahedron: 12 pentagons
Icosahedron: 20 equilateral triangles

In addition to the five Platonic Solids, there are also 13 so called "Archimedean Solids" which are formed by truncating (chopping off) the corners of each Platonic Solid. They are defined as "a solid which has plane faces that are all regular polygons though not all of the regular polygons are of the same species and each of which has all its polyhedral angles equal."

PROBLEM:
Using the above patterns, neatly construct all of the Platonic Solids.
Edges shall be all 2". Tabs are 1/4" wide and cut at an angle. Make each side separately, score tabs and glue together with Elmer's Glue-All. The last piece is the most difficult to glue. Compose the five solids as group to create balance and mount on a 20" x 20" base of FoamCore. No lettering is required.

MEDIA: Manila folder stock, 3/16" Foam Core board, Exacto knife, and Elmer's glue.